Class 6 Maths Chapter 3 Number Play Solutions

Number Play Class 6 Solutions Questions and Answers

3.1 Numbers can Tell us Things 3.2 Supercells Figure it Out (Page No. 57-58)

Question 1.
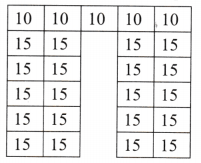
Colour or mark the supercells in the table below.

Solution:

Question 2.
Fill the table below with only 4-digit numbers such that the supercells are exactly the coloured cells.

Solution:

(Answer may vary)

Question 3.
Fill the table below such that we get as many supercells as possible. Use numbers between 100 and 1000 without repetitions.

Solution:

Question 4.
Out of the 9 numbers, how many supercells are there in the table above? _____________
Solution:
There are 5 supercells in the above table out of the 9 numbers.

Question 5.
Find out how many supercells are possible for different numbers of cells.
Do you notice any pattern? What is the method to fill a given table to get the maximum number of supercells? Explore and share your strategy.
Solution:
Do it yourself.

Question 6.
Can you fill a supercell table without repeating numbers such that there are no supercells? Why or why not?
Solution:
No, if we fill with numbers increasing by 1, we get at least one supercell, i.e., the last number.

Question 7.
Will the cell having the largest number in a table always be a supercell? Can the cell having the smallest number in a table be a supercell? Why or why not?
Solution:
Yes, the cell having the largest number in a table always be a supercell and the cell having the smallest number in a table will never be a supercell, as its adjacent cell has bigger number.

Question 8.
Fill a table such that the cell having the second largest number is not a supercell.
Solution:

Question 9.
Fill a table such that the cell having the second largest number is not a supercell but the second smallest number is a supercell. Is it possible?
Solution:
Yes, this is possible.

Question 10.
Make other variations of this puzzle and challenge your classmates.
Solution:
Do it yourself.
Note: For Solution:8-10, answer may vary.

InText Questions (Pages 58-59)

Question 1.
Complete Table 2 with 5-digit numbers whose digits are ‘1’, ‘0’, ‘6’, ‘3’, and ‘9’ in some order. Only a coloured cell should have a number greater than all its neighbours.

The biggest number in the table is _____________.
The smallest even number in the table is _____________.
The smallest number greater than 50,000 in the table is _____________
Solution:
Once you have filled the table above, put commas appropriately after the thousands digit.

96,310	96,301	36,109	36,910
13,690	13,609	60,319	19,306
13,906	10,936	60,193	19,360
10,369	10,963	10,396	19,630

The biggest number in the table is 96,310.
The smallest even number in the table is 10,396.
The smallest number greater than 50,000 in the table is 60,193. (Answer may vary)

 

3.3 Patterns of Numbers on the Number Line Figure it Out (Page No. 59)

Question 1.
Identify the numbers marked on the number lines below, and label the remaining positions.
Put a circle around the smallest number and a box around the largest number in each of the sequences above.

Solution:

Solution:

Solution:

Solution:

Intext Questions (Page 60)

Question 1.
Find out how many numbers have two digits, three digits, four digits, and five digits:

Solution:

3.4 Playing with Digits (Page No. 60)

Question 1.
Digit sum 14
(a) Write other numbers whose digits add up to 14.
(b) What is the smallest number whose digit sum is 14?
(c) What is the largest 5-digit whose digit sum is 14?
(d) How big a number can you form having the digit sum 14? Can you make an even bigger number?
Solution:
(a) 59, 68, 77, 86, 95, 149, 158, 167, 176, … (Answer may vary)
(b) 59, is the smallest number whose digit sum is 14.
(c) 95,000, is the largest 5-digit whose digit sum is 14.
(d) We can make an infinite number whose digit sum is 14.
For example: 11111111111111, 1111111111111100, 11111111111111000 and so on.
Yes, we can make an even bigger number having the digit sum 14.

Question 2.
Find out the digit sums of all the numbers from 40 to 70. Share your observations with the class.
Solution:
40 = 4 + 0 = 4
41 = 4 + 1 = 5
42 = 4 + 2 = 6
43 = 4 + 3 = 7
44 = 4 + 4 = 8
45 = 4 + 5 = 9
46 = 4 + 6 = 10
47 = 4 + 7 = 11
48 = 4 + 8 = 12
49 = 4 + 9 = 13
50 = 5 + 0 = 5
69 = 6 + 9 = 15
70 = 7 + 0 = 7,
Do it yourself

 

Question 3.
Calculate the digit sums of 3-digit numbers whose digits are consecutive (for example, 345). Do you see a pattern? Will this pattern continue?
Solution:
1 + 2 + 3 = 6,
2 + 3 + 4 = 9,
3 + 4 + 5= 12,
4 + 5 + 6 = 15,
5 + 6 + 7 = 18,
6 + 7 + 8 = 21,
7 + 8 + 9 = 24.
Yes, the pattern is a table of 3 from 3 × 2 to 3 × 8.
We cannot continue this pattern after 789.

InText Questions (Page 61)

Question 1.
Among the numbers 1-100, how many times will the digit ‘7’ occur? Among the numbers 1-1000, how many times will the digit ‘7’ occur?
Solution:
There are 10 numbers with 7 in the ones digit, i.e., 7, 17, 27, 37, 47, 57, 67, 77, 87, 97.
There are 10 numbers with 7 in the tens digit, i.e., 70, 71, 72, 73, 74, 75, 76, 77, 78, 79.
So, among the numbers 1-100, digit ‘7’ occur 20 times.
Similarly, from 101-200, 20 times digit ‘7’ occur.
201-300, 20 times digit ‘7’ occur.
301-400, 20 times digit ‘7’ occur.
401-500, 20 times digit ‘7’ occur.
501-600, 20 times digit ‘7’ occur.
601-700, 21 times digit ‘7’ occur.
801-900, 20 times digit ‘7’ occur.
901-1000, 20 times digit ‘7’ occur.

Now, from 701-800,
At hundred place of these 3 digit numbers, 7 will come 100 times.
At tens place 7 will come 10 times, i.e., 770, 771, 772, 773, 774, 775, 775, 777, 778, 779.
At units place 7 will come 10 times, i.e., 707, 717, 727, 737, 747, 757, 767, 777, 787, 797.
So, total number of times digit ‘7’ occurs from 701 – 800 = 100 + 10 + 10 = 120
By adding all, we get 20 × 8 + 120 + 21 = 301

Question 2.
Write all possible 3-digit palindromes using these digits.
Solution:
The possible 3-digit palindromes using the digit 1, 2, 3 are:
111, 121, 212, 131, 222, 232, 313, 323, 333.

InText Questions (Page 62)

Question 1.
Puzzle time

I am a 5-digit palindrome.
I am an odd number.
My ‘t’ digit is double of my ‘u’ digit.
My ‘h’ digit is double of my ‘t’ digit.
Who am I? _______
Solution:

The required 5-digit od d palindrome number is 12421, where ‘t’ digit is double of ‘u’ digit and ‘h’ digit is double of‘t’ digit.
In words: Twelve thousand four hundred twenty-one.

InText Questions (Page 64)

On the usual 12-hour clock, there are timings with different patterns. For example, 4:44, 10:10, 12:21.

Question 1.
Try and find out all possible times on a 12-hour clock of each of these types.
Solution:
Possible times on a 12-hour clock are as follows: 1:11, 2:22, 11:11, 4:44, 01:01, 12:21 and so on.
Manish has his birthday on 20/12/2012, where the digits ‘2’, ‘0’, ‘ 1 ’ and ‘2’ repeat in that order.

Question 2.
Find some other dates of this form from the past.
Solution:
Possible dates of the form 20/12/2012, where the digits ‘2’, ‘0’, ‘ 1 ’, and ‘2’ repeat in that order are as follows: 12/01/1201, 19/10/1910, 20/11/2011 and so on.
His sister Meghana has her birthday on 11/02/2011 where the digits read the same from left to right and from right to, left.

 

Question 3.
Find all possible dates of this form from the past.
Solution:
Possible dates of the form 11/02/2011, where the digits read the same from left to right and from right to left are as follows:
10/02/2001, 09/01/1090, 08/02/2080
Jeevan was looking at this year’s calendar. He started wondering, “Why should we change the calendar every year!
Can we not reuse a calendar?” What do you think?
You might have noticed that last year’s calendar was different from this year’s. Also, next year’s calendar is also different from the previous years.

Question 4.
But, will any year’s calendar repeat again after some years? Will all dates and days in a year match exactly with that of another year?
Solution:
Calendar repetition can happen after 6 or 11 years, depending on the leap year. Leap years have 366 days, so these calendars are the same every 28 years.
For example, the 2024 calendar will repeat in 2052, and the 2022 calendar will repeat in 2033.
Yes, all dates and days in a year match exactly with that of another year.

3.5 Pretty Palindromic Patterns 3.6 The Magic Number of Kaprekar 3.7 Clock and Calendar Numbers Figure it Out (Page No. 64-65)

Question 1.
Pratibha uses the digits ‘4’, ‘7’, ‘3’ and ‘2’, and makes the smallest and largest 4-digit numbers with them: 2347 and 7432. The difference between these two numbers is 7432 – 2347 = 5085. The sum of these two numbers is 9779. Choose 4-digits to make:
(a) the difference between the largest and smallest numbers greater than 5085.
(b) the difference between the largest and smallest numbers less than 5085.
(c) the sum of the largest and smallest numbers greater than 9779.
(d) the sum of the largest and smallest numbers less than 9779.
Solution:
(a) 5, 8, 3, 2; largest 4-digit number: 8532, smallest 4- digit number: 2358 Difference: 8532 – 2358 = 6174 > 5085
(b) 4, 6, 3, 2; largest 4-digit number: 6432, smallest 4- digit number = 2346 Difference: 6432 – 2346 = 4086 < 5085
(c) 5, 8, 3, 2 → 8532 + 2358 = 10890 > 9779
(d) 4, 6, 3, 2 → 6432 + 2346 = 8778 < 9779
(Answers may vary)

Question 2.
What is the sum of the smallest and largest 5-digit palindrome? What is their difference?
Solution:
Largest 5-digit palindromic number = 99999
Smallest 5-digit palindromic number = 10001
Sum = 99999 + 10001 = 110000
Difference = 89998

Question 3.
The time now is 10:01. How many minutes until the clock shows the next palindromic time? What about the one after that?
Solution:
Next palindromic time after 10:01 is 11:11 after 70 minutes. After that next palindromic time will be 12:21.

 

Question 4.
How many rounds does the number 5683 take to reach the Kaprekar constant?
Solution:
Given number: 5683

Hence, the number 5683 takes 8 rounds to reach the Kaprekar constant.

InText Questions (Page 66)

Question 1.
Can we make 1,000 using the numbers in the middle? Why not? What about 14,000, 15,000 and 16,000? Yes, it is possible. Explore how. What thousands cannot be made? (Refer the figure on page 65 of NCERT Textbook)
Solution:
Yes, we can make 1000 using the numbers in the middle.
1000= 1500 – 400 – 400 – 4
14000 = 13000 + 400 × 2 + 400 = 2
15000 = 13000 + 400 × 4 + 400
16000= 13000 + 1500 × 2

3.8 Mental Math Figure it Out (Page No. 66 – 67)

Question 1.
Write an example for each of the below scenarios whenever possible.

Could you find examples for all the cases? If not, think and discuss what could be the reason. Make other such questions and challenge your classmates.
Solution:

5-digit + 5-digit to give a 5-digit sum more than 90,250	1st 5-digit number: 23,456 2nd 5-digit number: 66,795 Sum = 23,456 + 66,795 = 90251 >90250.
5-digit + 3-digit to give a 6-digit sum	5-digit number: 99,456 3-digit number: 795 Sum = 99,456 + 795 = 1,00,251 (a 6-digit sum).
4-digit + 4-digit to give a 6-digit sum	Not possible, because if we take both the numbers as largest 4-digit number 9999, then the sum = 9999 + 9999 = 19,998; a 5-digit sum.
5-digit + 5-digit to give a 6-digit sum	1st 5-digit number: 63,456 2nd 5-digit number: 66,795 Sum = 63,456 + 66,795 = 1,30,251; a 6-digit sum.
5-digit + 5-digit to give 18,500	Not possible, because if we take the 1st 5-digit number as the smallest 5-digit number, i.e., 10,000, then, the second number will be 8,500 to get the required sum; which is a 4-digit number.
5-digit – 5-digit to give a difference less than 56,503	1st 5-digit number: 93,456 2nd 5-digit number: 36,995 Difference = 56,461 < 56,603.
5-digit – 3-digit to give a 4-digit difference	5-digit number: 10,000 3-digit number: 999 Difference = 10,000 – 999 = 9,001; a 4-digit difference.
5-digit – 4-digit to give a 4-digit difference	5-digit number: 10,000 4-digit number: 1,000 Difference = 10,000 – 1,000 = 9,000; a 4-digit difference.
5-digit – 5-digit to give a 3-digit difference	1st 5-digit number: 60,456 2nd 5-digit number: 60,195 Difference = 60,456 – 60,195 261, a 3-digit difference.
5-digit – 5-digit to give 91,500	Not possible, because if we get the required difference we take the 1st 5-digit number, that will be the largest 5-digit number, i.e., 99,999 and the second number will be a 4-digit number ‘8499’.

(Answer may vary)
For further do it yourself.

Question 2.
Always, Sometimes, Never?
Below are some statements. Think, explore and find out if each of the statement is ‘Always true’, ‘Only sometimes true’ or ‘Never true’. Why do you think so? Write your reasoning; discuss this with the class.
(a) 5-digit number + 5-digit number gives a 5-digit number
(b) 4-digit number + 2-digit number gives a 4-digit number
(c) 4-digit number + 2-digit number gives a 6-digit number
(d) 5-digit number – 5-digit number gives a 5-digit number
(e) 5-digit number – 2-digit number gives a 3-digit number
Solution:

5-digit number + 5-digit number gives a 5-digit number	Only Sometimes true	If we take the 1st 5-digit number: 13,456 2nd 5-digit number: 56,795 Then sum =13,456 + 56,795 = 70,251 (a 5-digit number), But if we take the 1st 5-digit number: 13,456, 2nd 5-digit number: 96,795 Then sum = 13,456 + 96,795 = 1,10,251 (a 6-digit number).
4-digit number + 2-digit number gives a 4-digit number	Only Sometimes true	If we take the 4-digit number: 3,456 2-digit number: 95 Then sum = 3,456 + 95 = 3,551 (a 4-digit number), But if we take the 4-digit number: 9,999 2-digit number: 95 Then sum = 10,094 (a 5-digit number).
4-digit number + 2-digit number gives a 6-digit number	Never true	If we even take the largest digit number: 9,999 and largest 2-digit number: 99 Then sum = 9,999 + 99 = 10,098 (a digit number).
5-digit number – 5-digit number gives a 5-digit number	Only Sometimes true	If we take the 1 st 5-digit number: 2nd 5-digit number: 16,795. Then the difference = 53,456 – 16,795 = 36,661 (a 5-digit number), But if we take the 1st 5-digit number: 2nd 5-digit number: 11,795 Then the difference = 13.456 – 11,795 = 1,661 (a 4-digit number).
5-digit number – 2-digit number gives a 3-digit number	Never true	If we take the smallest 5-digit number: 10,000 and the largest 2-digit number: 99 Then the difference = 10,000-99 = 9,901 (a 4-digit number).

InText Questions (Pages 67-68)

Question 1.
Share and discuss in class the different methods each of you used to solve these questions.

Solution:
Sum of numbers = 12 × 40 + 10 × 50 = 480 + 500 = 980

 

Solution:
Sum of numbers = 44 × 1 + 20 × 5 = 144

 

Solution:
Sum of numbers = 32 × 32 + 16 × 64 = 1024 + 1024 = 2048

Solution:
Sum of numbers = 17 × 3 + 18 × 4 = 51 + 72 = 123

Solution:
Sum of numbers = 15 × 22 + 25 × 22 + 35 × 22 = 330 + 550 + 770= 1650

Solution:
Sum of numbers = 18 × 125 + 8 × 250 + 4 × 500 + 1000 = 2250 + 2000 + 2000 + 1000 = 7250

InText Questions (Page 69)

Question 1.
Make some more Collatz sequences like those above, starting with your favourite whole numbers. Do you always reach 1?
Solution:
Collatz sequence starting with whole number 15 is as follows:
15,46,23,70,35,106,53,160,80, 40,20,10,5,16,8,4,2,1.
Collatz sequence starting with whole number 7 is as follows:
7,22,11,34,17,52,26,13,40,20,10,5,16,8,4,2,1.

 

3.9 Playing with Number Patterns Figure Out(Pages.no 69 – 70)

Question 1.
We shall do some simple estimates. It is a fun exercise, and you may find it amusing to know the various numbers around us. Remember, we are not interested in the exact numbers for the following questions. Share your methods of estimation with the class.

1. Steps you would take to walk:
(a) From the place you are sitting to the classroom door
(b) Across the school ground from start to end
(c) From your classroom door to the school gate
(d) From your school to your home

2. Number of times you blink your eyes or number of breaths you take:
(a) In a minute
(b) In an hour
(c) In a day

3. Name some objects around you that are:
(a) a few thousand in number
(b) more than ten thousand in number
Solution:
Do it yourself.

3.10 An Unsolved Mystery – the Collatz Conjecture! 3.11 Simple Estimation 3.12 Games and Winning Strategies Figure it Out (Page No. 72 – 73)

Question 1.
There is only one supercell (number greater than all its neighbours) in this grid. If you exchange two digits of one of the numbers, there will be 4 supercells. Figure out which digits to swap.

Solution:
If we swap the digits, 6 and 1 of 62,871, we get the 4 supercells.

Question 2.
How many rounds does your year of birth take to reach the Kaprekar constant?
Solution:
Do it yourself.

Question 3.
We are the group of 5-digit numbers between 35,000 and 75,000 such that all of our digits are odd. Who is the largest number in our group? Who is the smallest number in our group? Who among us is the closest to 50,000?
Solution:
5-digit numbers between 35,000 and 75,000 such that all of our digits are odd are as follows:
35,111, 35,113; 35,115; 35,117; 35,119; …; 39,999; 51,111; 51,113; …; 73,999.
So, the largest number of the group = 73,999
and, the smallest number of the group = 35,111
∴ The number closest to 50,000 = 51,111

Question 4.
Estimate the number of holidays you get in a year including weekends, festivals and vacation. Then try to get an exact number and see how close your estimate is.
Solution:
Do it yourself.

Question 5.
Estimate the number of liters a mug, a bucket and an overhead tank can hold.
Solution:
Mug: 1 litre
Bucket: 20 litre
Overhead tank: 20,000 litre (Answer may vary)

Question 6.
Write one 5-digit number and two 3-digit numbers such that their sum is 18,670.
Solution:
Let the 5-digit number = 18,000
And the 1st 3-digit number = 345
The 2nd 3-digit number = 325
So, their sum = 18,000 + 345 + 325 = 18,670 (Answer may vary)

Question 7.
Choose a number between 210 and 390. Create a number pattern similar to those shown in Section 3.9 that will sum up to this number.
Solution:
Let the number be 350.
Corresponding number pattern:

Question 8.
Recall the sequence of Powers of 2 from Chapter 1, Table 1. Why is the Collatz conjecture correct for all the starting numbers in this sequence?
Solution:
The sequence of powers of 2 is as follows: 1,2, 4, 8, 16, 32, 64,…
Since,

• if the sequence starts with 2, an even number then half of it is 1.
• if the sequence starts with 4, an even number then half of it is 2 and further its half is 1.
• if the sequence starts with 8, an even number then half of it is 4, further its half is 2 and further 1.
• In the same way if the sequence is starts with 64, then half of it is 32, and further the sequence is as follows: 64, 32, 16, 8, 4, 2, 1.

Hence, the Collatz Conjecture rule is correct for all the starting numbers in this sequence.

 

Question 9.
Check if the Collatz Conjecture holds for the starting number 100.
Solution:
As per Collatz Conjecture rule: starts with any number; if the number is even, take half of it; if the number is odd, then multiply it by 3 and add 1; and repeat.
The sequence formed with starting number 100 is as follows:
100, 50, 25, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.
Hence, the Collatz Conjecture holds for the starting number 100.

Question 10.
Starting with 0, players alternate adding numbers between 1 and 3. The first person to reach 22 wins. What is the winning strategy now?
Solution:
Do it yourself.